スパースモデリングによる高次元データ駆動科学の創成

より深く自然を知りたいという飽くなき探究心が，とどまることを知らない計測技術の向上をもたらし，大量の高次元観測データを日々生み続けている． この状況において，科学技術の水準を革新的に向上・強化させるためには，情報科学と自然科学が緊密に融合した革新的な自然探究の方法論が必要不可欠である．我々は，その方法論構築のためのキーテクノロジーが，近年，情報科学分野で大きな注目を集めているスパースモデリングであると考える．スパースモデリングは，高次元データに普遍的に内在するスパース(疎)性を利用することで，計算量が次元数に対して指数爆発(計算量爆発)する状況でも，実際的時間でデータから最大限の情報を効率よく抽出できる技術の総称である．これまでもスパースモデリングは個別分野において萌芽的成果を生み出しており，それらの背後にある共通原理を明確化し，より強力なものにすることは自然科学全体に革新的展開をもたらす．

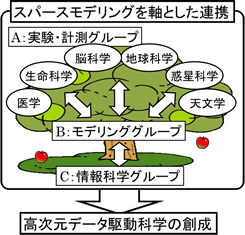
こうした現状認識を踏まえ，本領域では，スパースモデリングや高次元データ解析で顕著な実績をあげている情報科学者と，生命分子からブラックホールに至る，幅広い自然科学の実験・計測研究者がスパースモデリングというキーテクノロジーを軸として緊密に連携することで，大量の高次元データを効率的に科学的な知へとつなげる高次元データ駆動科学ともいうべき新学術領域を創成する．これにより，これまで，個々の分野ごとに探求されていた課題に対して，新たな共通原理に基づく革新的な科学的方法論を確立することによって，あらゆる科学分野の研究に大きな波及効果をもたらし，来たるべきデータ科学の時代に向けて，我が国の学術水準の優位性を確立する．

その具体化へ向けて，以下の三つの重点目標を掲げる．

A：データ駆動型科学の実践：高次元データの効率的な活用により，科学的方法の質的変化を引き起こすことで，自然科学の個別の課題を解決する．

B：モデリング原理の確立：多様な視点の導入により，分野の個別性を超えた類似性／共通性にもとづいた対象／現象のモデル化法に関する理論整備を行うことで，革新的展開を生み出す．

C：数理基盤の形成：非線形で不確実性を伴う高次元の自然科学データに関して，具体的事例から数理的課題を絞り込むことで，実証的観点から従来の多変量解析理論を刷新する．

これらA, B, Cに対して，実験・計測グループ(実験G，A01,A02)，モデリンググループ(モデルG，B01)，情報科学グループ(情報G，C01)の三つの項目をおく．自然科学と情報科学の緊密な連携・融合を目指す本領域において，モデルG(B01)のインターフェース・触媒としての役割が特に重要である．モデルG(B01)は構造的類似性に基づき，できるだけ一般性を持ったモデリング原理の確立を目指す横断的コーディネーション研究を中心的機能として研究を進める．

なぜスパースモデリングか？

科学とは，(1)研究者の仮説や意図に基づいた実験・観測によりデータを獲得し，(2)そこから少数の説明変数を選択し，(3)得られた説明変数と仮説を比較し対応することで法則を発見する行為である．この仮説の提案／検証ループの不断の繰り返しにより今日の科学は発展してきた．天体観測の結果を分析し，ケプラーの法則を経て到達したニュートン力学はこの模範例である．一方で，近年の計測技術の発展によるデータの高次元化で計算量が爆発する状況に，研究者の直感的行為である思索や試行錯誤が追いつかずに，こうした仮説／検証ループにもとづくモデル化が著しく困難になっている．こうした問題は，物理学や化学と比して，多数の要素が生み出す複雑な現象に目を向ける生物や地学など「理科第2分野」に分類される科学で特に顕著である．

スパースモデリングとはこのような困難を解決するために提案されたモデル化の総称である．その基本的な考え方は(1)高次元データの説明変数が次元数よりも少ない(スパース(疎)である)と仮定し，(2)説明変数の個数がなるべく小さくなることと，データへの適合とを同時に要請することにより，(3)人手に頼らない自動的な説明変数の選択を可能にする枠組みである．スパースモデリングの先駆は1980年代の後半に石川真澄（九工大）が提案した人工神経回路網モデルの「忘却付き構造学習」であり，1990年代半ばTibshirani（Stanford大）が提案したLASSO推定法やTippingとBishop（Microsoft研究所）のARD法などを契機として生命情報科学，データマイニングの分野でその有用性が広く認知されるようになった．さらに，2000年代半ばからはDonoho（Stanford大）らが提唱している圧縮センシング(CS)が計測工学，通信工学，医用工学，生化学など幅広い分野で革新的情報抽出技術として大きな注目を集めている．

何をどこまで明らかにしようとするのか

実験G(A01, A02)では，第一原理からのモデル化が難しい生物学，地学などの理科第２分野を中心に，大量の高次元データの有効活用による新規な規則発見や実験プロトコルの飛躍的高速化を実現する科学的方法を確立することで，ブレークスルーを起こす．その一例は，A02-3班(計画代表：本間)が，電波干渉計データからSMを用いて，回折限界の3-4倍の超解像を達成し，想像されているブラックホールの直接撮像という天文学・天体物理学史上最大級のマイルストーンを刻みこむことである(Science, Online September 27 2012)．

その他にも，医学分野ではMRIの計測手法自体を革新し計測時間を半分以下へ短縮，患者の負担の大幅減を目指す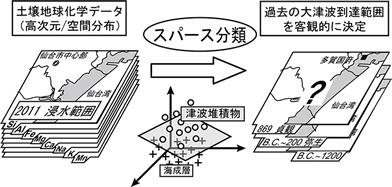． 生命科学分野では，NMRの測定時間を数日から数時間に短縮し，タンパク質の立体構造推定の研究の質的変化を目指す．脳科学分野では側頭葉でのパターン認識機構を解明し，脳科学と情報科学の変革を目指す．地球科学分野では，高次元の地球化学データから，津波堆積物を特徴づける少数の元素を抽出し，緊急性の高い東北地域の津波到達範囲の予測を目指す．

モデルG(B01)は，分野横断的な数理構造の類似性に基づき，自然科学の個別データと情報科学の汎用的解析を結ぶシステム科学的方法論を探究することで，仮説／検証ループに基づくモデル化を系統的に行う普遍的枠組みを提案する．これにより，分野の垣根を越えたアナロジーや普遍性を個別問題の解決に活用するデータ駆動型普遍的現象論ともいうべき接近法を確立する．

情報G(C01)では，実際的な状況の特徴を取り入れられる典型モデルを開発し，ガウス性に強く依存していた従来の多変量解析の方法を刷新し，SMの数理的基盤を確立する．そのために自然科学データの解析に必要な技術である，非線形性や階層性の取り扱い(非線形, C01-1)，従来の枠組みではモデル化しにくい状況のモデル化(セミパラメトリックベイズ, C01-2)，高次元化による計算困難の打破(大自由度, C01-3)を担当する三つの計画研究をおいた．また，仮説／検証ループを効率的に稼働させるために，解析結果をわかりやすく実験者にフィードバックする手法を開発する(可視化, C01-4)．また，モデルG(B01)と実験G(A01,A02)の密接な連携は，対象とする系それぞれに対し，科学の本質である仮説／検証ループに基づく最適なモデリングを可能にし，ポストプロセス中心のデータ解析から脱却することにより，自然科学データから最大限に科学的知見を抽出する．