(B01-1)
Compressed sensing is a prominent example of sparse modeling in which a small number of essential variables for description of a given phenomenon are extracted based on data, and it is currently being examined for application in a wide range of fields. Compressed sensing is a framework that enables extraction of the essential background structure of a phenomenon from a small number of acquired data. Researchers around the world are competing to develop specific applications and to improve the performance of the framework.
The plan for this project is to formulate a new compressed sensing framework based on an original concept targeting wide-ranging applications. The framework will be developed from a multidisciplinary perspective, by coordinating in particular with the (A01-1), the (A01-2), and the (A02-3), and using various observational data.
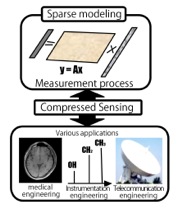
As measurement technologies have been improved, large quantities of high-dimensional data have been collected in various fields of natural science. Although the collected data may live in a high-dimensional space, the essential dimension is low in many cases. The recently proposed compressed sensing framework is able to extract the essential structure of the high-dimensional data from small amount of observed data, and as such, it is a prominent example of sparse modeling. In a short time, it has been considered for application in a wide range of fields such as instrumentation engineering, telecommunications engineering, and medical engineering, where its efficacy has generated considerable interest.
Tanaka and others have lead the world in focusing on the potential of compressed sensing from an early stage and have successfully analyzed the theoretical bounds of compressed sensing from the perspective of the statistical mechanics. Tanaka and Ikeda have lead the world in mathematical research related to compressed sensing and sparse modeling, including MRI reconstruction algorithms and methods for phase recovery of X-ray diffraction images.
Moreover, Tanaka and Ikeda have tested applications for compressed sensing from their perspectives in the specific cases of super resolution exceeding the resolution limit of high-speed MR imaging and very-long-baseline interferometry (VLBI), respectively. In the process, they have come to realize that it is of utmost importance to model the actual measurement process and other aspects properly, to resolve them with an appropriate algorithm, and to consider multiple application examples in a cross-disciplinary manner.
The present plan of the project involves a detailed study of individual cases where sparse modeling by compressed sensing should be effective. The topics will be taken under the collaboration with the (A01 and A02: (A01-1), (A01-2), and (A02-3)) as well as individual researches which will join to the program. This stands in a cross-disciplinary perspective viewpoint. For each individual case, the aim of our research is to fill the gap between the scientific goal and the measurements with an appropriate mathematical treatment. This cross-disciplinary approach is expected to establish not only a new method for individual cases, but also to build a general framework for high-dimensional data analysis.
- [Subject 1] Tailored compressed sensing researches
This subject will investigate the effectiveness and range of application of compressed sensing by focusing on specific topics including but not limited to the magnetic resonance imaging (MRI) by the (A01-1), the nuclear magnetic resonance (NMR) spectroscopy by the (A01-2), the very long baseline interferometry (VLBI) by the (A02-3). - [Subject 2] Introduction of Bayesian inference to compressed sensing
By monitoring the observation process associated with individual applications, the research will construct an applicable Bayesian inference framework to enhance performance. - [Subject 3] Cross-disciplinary research on the mathematical properties of compressed sensing
This subject will investigate the mathematical properties of compressed sensing from a cross-disciplinary viewpoint based on the individual formulations for each problem field, but without limiting the discussion to individual theories.
