スパースモデリング班(B01-2)

研究課題名：スパースモデリングによる潜在構造の抽出

研究概要

大量の高次元観測データが得られる一方で，データの肥大化により，研究者の直感的行為である思索や試行錯誤が追いつかなくなっている．そのため，仮説／検証ループにもとづくモデル化が著しく困難になっている．

本計画研究では，高次元データに内在するスパース性を利用するスパースモデリング(SM)により，系の物理的な性質を仮定せず，生物学・地学における実験・計測データから，系の潜在構造としての物理特性を抽出する普遍的手法を開発する．これは情報理論の観点では，実験・計測データのデータ圧縮(情報源符号化)に対応する．これにより，分野の個別性を超えた類似性／共通性にもとづいたモデリング原理の確立と，種々の自然科学の状況に応じて柔軟に対処できる自然界の符号理論の構築をめざす．

本研究に関連する国内・国外の研究動向及び位置づけ

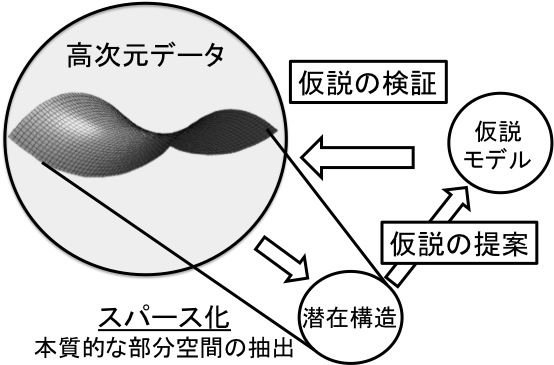今日の科学は，仮説に基づき実験・観測を行い，得られたデータから少数の説明変数を選択し，その説明変数と仮説を比較し対応するという，仮説の提案／検証ループの不断の繰り返しにより発展してきた．

近年の計測技術の向上によるデータの肥大化により，こうした仮説／検証ループにもとづくモデル化が著しく困難になっている．スパースモデリング(SM)とはこのような困難を解決するために提案されたモデル化／アルゴリズムの総称である．SMの先駆は1980年代の後半に石川真澄が提案した人工神経回路網モデルの忘却付き構造学習である．2000年代半ばからは圧縮センシング(CS)が計測工学など幅広い分野で革新的技術として大きな注目を集めている．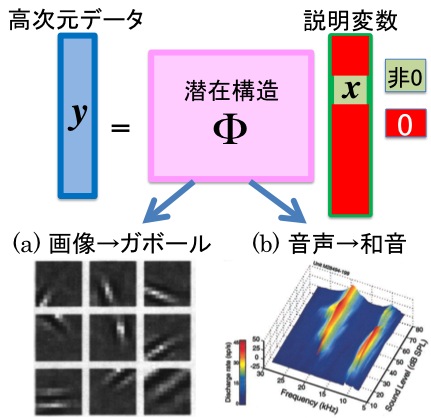

これまでの研究成果を踏まえ，着想に至った経緯

SMを自然画像のデータ圧縮に適用すると，右図(a)のように，JPEG2000に用いられるガボール関数が潜在構造Φとして抽出される(Olshausen and Field, 1996)．我々は音声信号にSMを適用し，潜在構造Φとして，マーモセットの聴覚一次野(A1)の反応特性(右図(b), Kadia and Wang, 2003)にも符合するハーモニー(和音)を自動抽出することに成功した(Terashima et al., 2013)．これらの知見から，外界のモデルを陽に知らない我々生物が外界の本質である潜在構造を知る方略として，SMを進化の過程で獲得したと考えることができる．さらに，SMによるデータ圧縮が自然科学における高次元データから潜在構造であるモデルを抽出する普遍的枠組みであるという着想に至った．

本計画研究の目的

本計画研究は，SMにより潜在構造を抽出する普遍的手法を開発し，分野の個別性を超えた類似性／共通性に基づく高次元データ駆動科学におけるモデリング原理の確立を目指す．具体的に，今後5年間で飛躍的発展が確実視される三つの課題を行う．

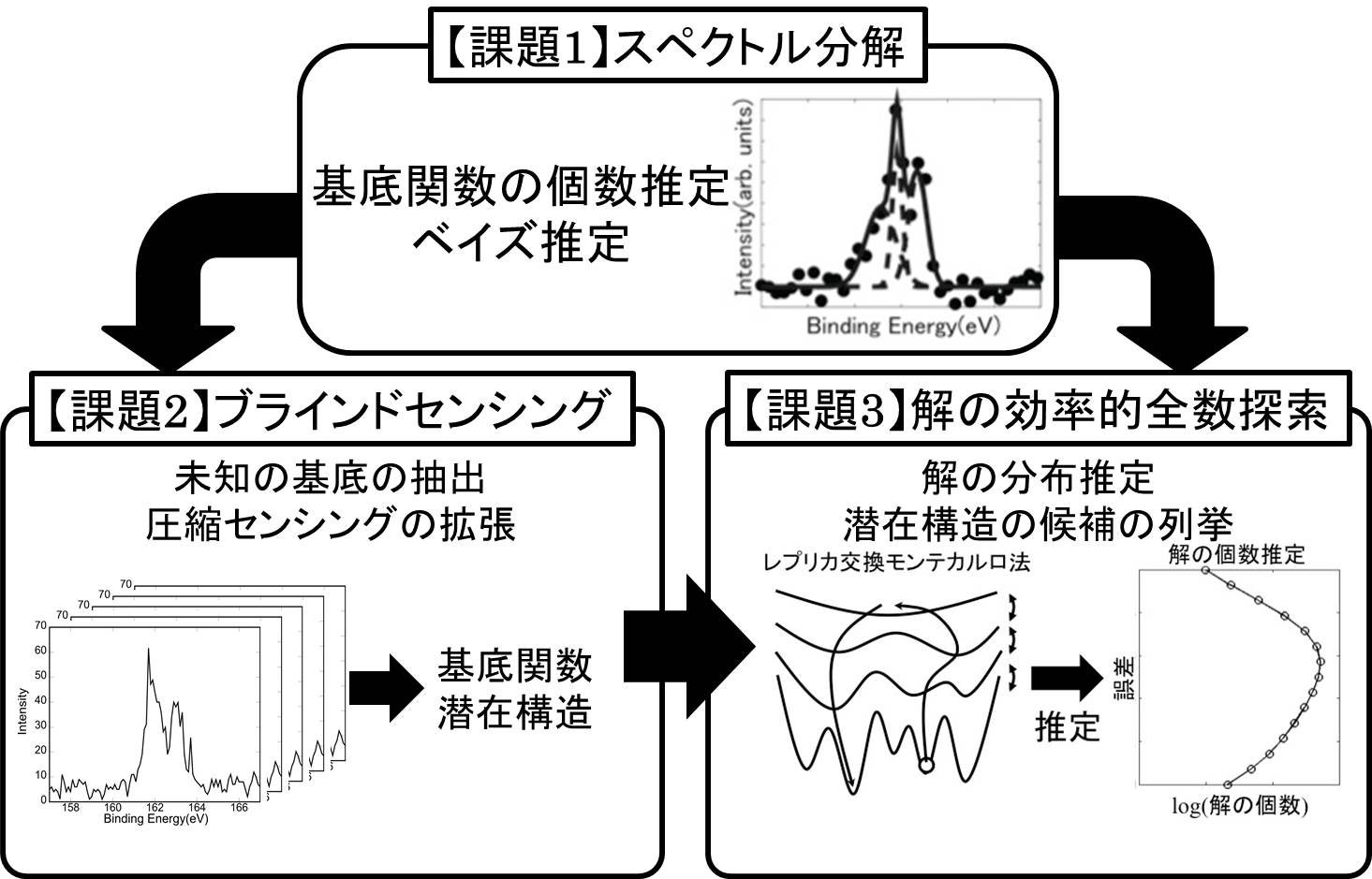
【課題1】スペクトル分解を用いたモデリング

多峰性スペクトルを適切な個数の単峰性の基底関数の線形和に分解する問題は，数理統計学の難問の一つである特異モデルの一つであり，X線光電子分光法(XPS)，NMR，光の反射スペクトル解析など，あらゆる自然科学の計測でも必要不可欠である．本課題では，このスペクトル分解の問題をSMにより解決する系統的方法論を構築する．

【課題2】ブラインドセンシング(BS)を用いたモデリング

上で述べたように潜在構造Φの構造はブラインドセンシング(BS)と呼ばれている．潜在構造Φをデータのみから抽出するセミパラメトリックな枠組みであるBSを多量のデータに適用し，その背後にある物理特性の自動抽出を目指す．その過程で情報科学グループ(C01)と協同し，情報幾何，代数幾何などの数学の枠組でBSの数理的枠組を深化させる．

【課題3】モンテカルロ法による高速全数検索を用いたモデリング

データの高次元化による自由度の増加により，計算機科学の充足可能性問題(SAT)と同様に，最適な基底の組み合わせが複数存在するケースに遭遇する．これをレプリカ交換モンテカルロ法により解決し，地球科学班(A02-1)の津波堆積物解析などに応用する．