(B01-2)
Although it has become possible to obtain large quantities of high-dimensional observation data, this data bloat makes it harder for researchers to follow their intuition and perform experimentation through trial and error. It is therefore becoming very difficult to perform modeling based on a hypothesis and test cycle.
In this , we use sparse modeling, which exploits the inherent sparseness of high-dimensional data, to develop a general method for the extraction of physical characteristics as latent structures of a system from experimental and measurement data in the fields of life science and geoscience without making any assumptions about the physical properties of a system. From an information theory viewpoint, this corresponds to compression (source coding) of the experimental and measurement data. In this way, we aim to establish modeling principles based on similarities and commonalities between disparate fields, and to construct a coding theory for the natural world that can adapt flexibly to situations in a wide variety of natural sciences.
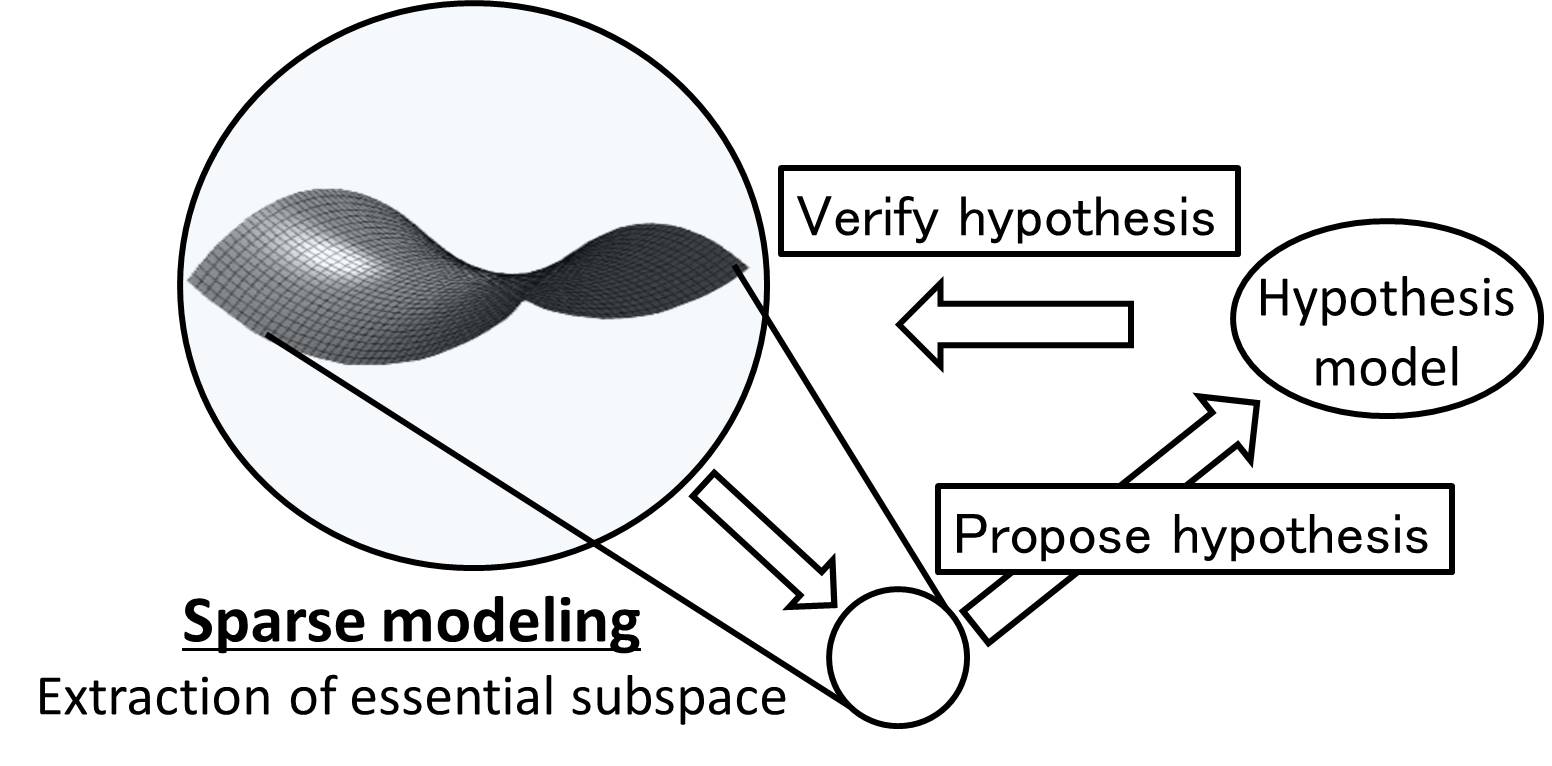Modern science has evolved through the unceasing repetition of a hypothesis and test cycle whereby experiments and observations are performed based on a hypothesis, a small number of explanatory variables are selected from the resulting data, and these explanatory variables are compared against the hypothesis.
In recent years, improvements in measurement technology have resulted in data bloat that makes it very difficult to perform modeling based on this sort of hypothesis and test cycle. Sparse modeling is a generic term for modeling methods and algorithms that have been proposed to resolve such difficulties. The precursor of sparse modeling was a neural network model called "structural learning with forgetting", which was proposed in the late 1980s by Masumi Ishikawa. Since the mid 2000s, a lot of attention has been drawn towards an innovative technique called compressed sensing (CS), which can be used in various fields including measurement engineering.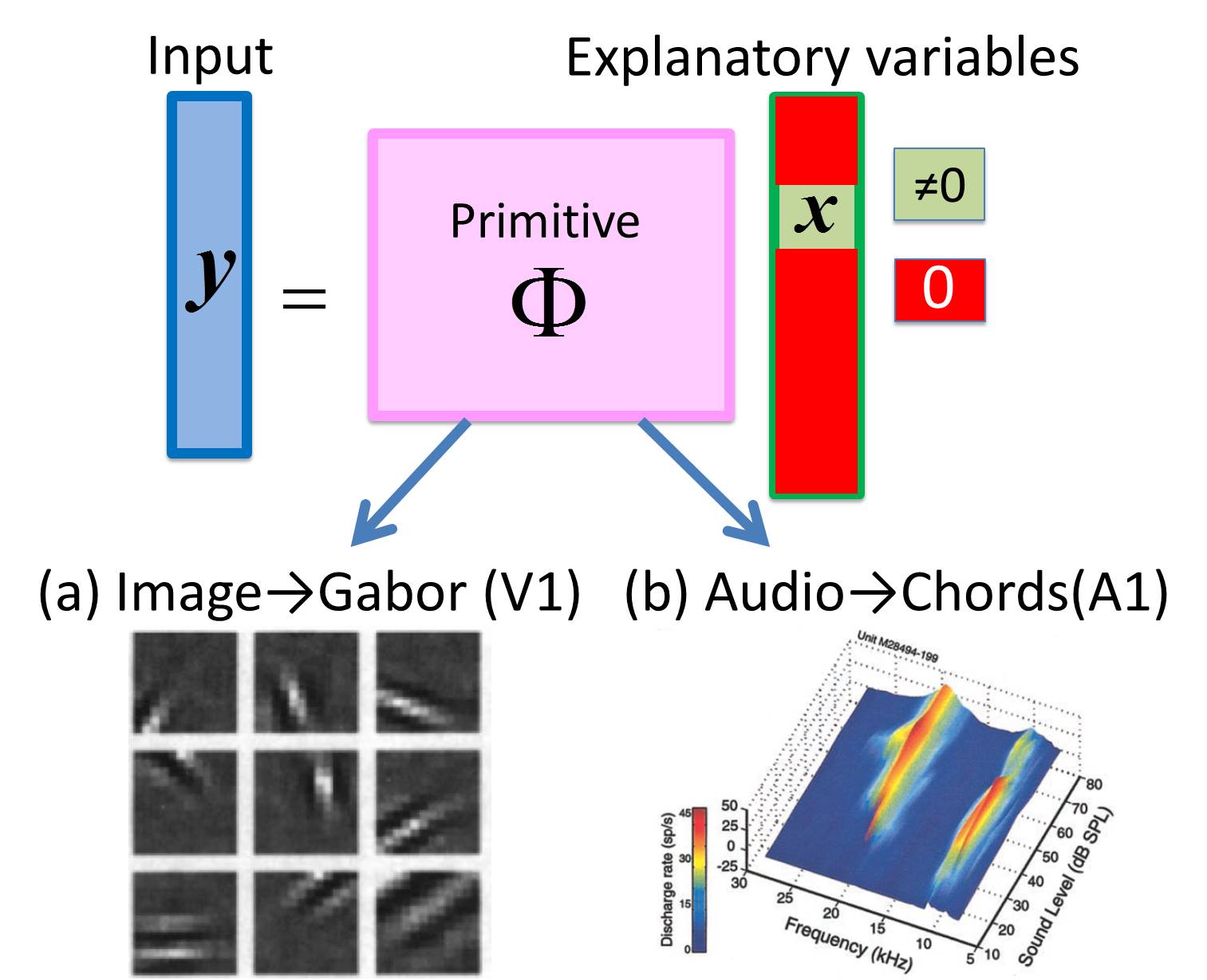
When sparse modeling is applied to data compression in natural images, the Gabor function used in JPEG2000 compression is extracted as a latent structure Φ (Olshausen and Field, 1996). By applying sparse modeling to audio signals, we succeeded in the automatic extraction of coincidental harmonies from the reaction characteristics of the primary auditory cortex of marmosets (A1) (on right (b), Kadia and Wang, 2003) (Terashima et al., 2013). These findings suggest that sparse modeling was acquired during the course of evolution as a strategy for understanding latent structures, which is the essence of how living organisms such as ourselves understand the outside world without having an explicit model. This also led us to the idea that data compression by sparse modeling is a general framework for the extraction of models (latent structures) from high-dimensional data in natural sciences.
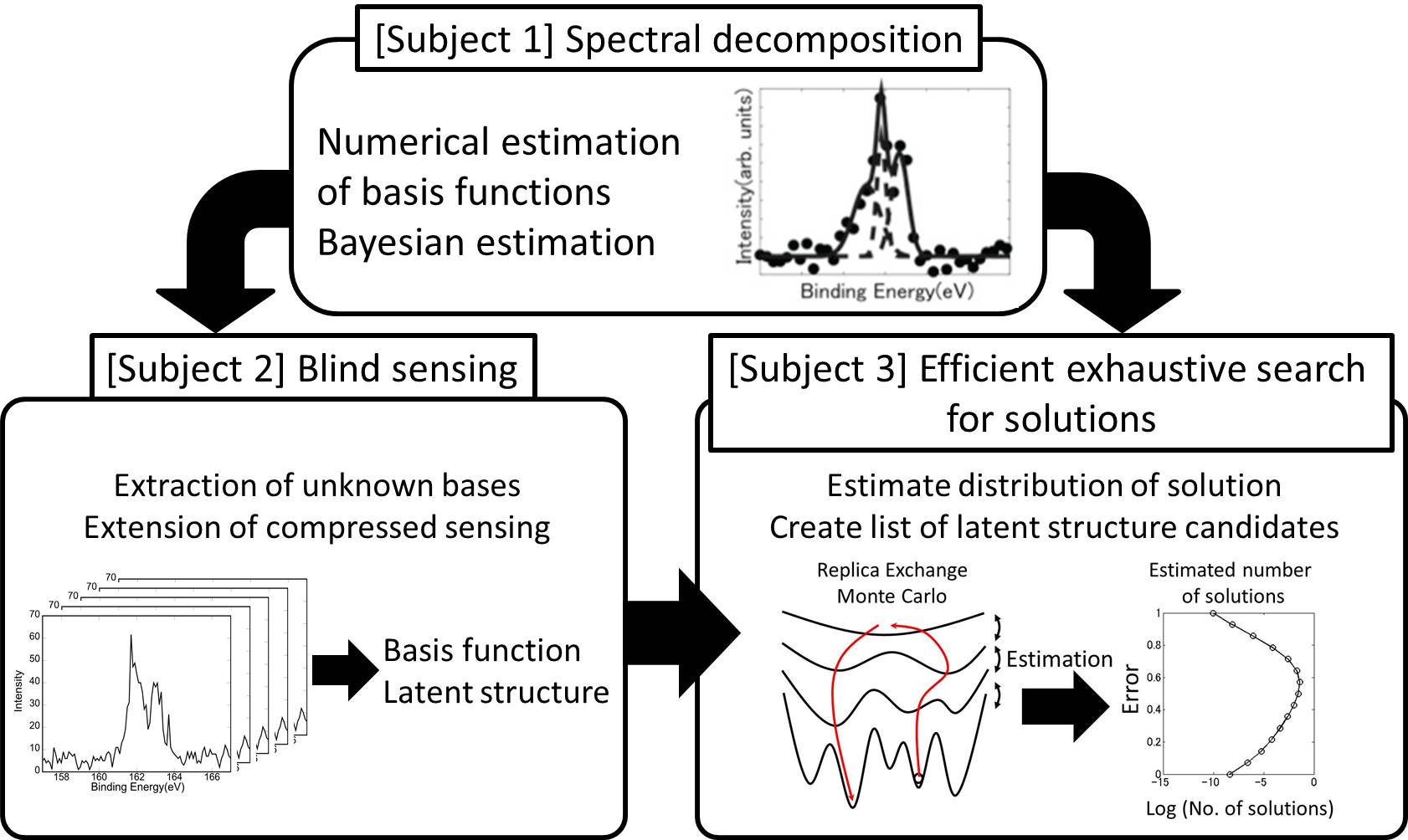
This aims to develop general methods for the extraction of latent structures by sparse modeling, and to establish modeling principles in data-driven science based on similarities and commonalities between disparate fields. Specifically, it addresses the following three subjects that look set to undergo rapid development over the next five years:
- [Subject 1] Modeling using spectral deconvolution
The problem of decomposing a multimodal spectrum into the linear sum of a suitable number of monomodal basis functions is a type of singular model, (a difficult problem in statistical mathematics), which has important significance in many different fields including X-ray photoelectron spectroscopy (XPS), NMR, optical reflectance spectroscopy and reflection spectral analysis. For this subject, we will construct a systematic methodology by using sparse modeling to solve this spectral deconvolution problem. - [Subject 2] Modeling using blind sensing (BS)
As mentioned above, the structure of a latent structure Φ is called blind sensing (BS). Our aim is to use BS (a semi-parametric framework) for the extraction of latent structure Φ from the data alone, and to automatically extract the physical properties in the background. In this process, we are cooperating with the (C01) to deepen the mathematical framework of BS with math frameworks such as information geometry and algebraic geometry. - [Subject 3] Modeling using a high-speed exhaustive search according to the Monte Carlo method
The increased degrees of freedom in high-dimensional data can lead to satisfiability problems (SAT) in computer science, and also to cases where there is more than one optimal combination of bases. This is resolved by using the replica exchange Monte Carlo method, which is applied to problems such as the analysis of tsunami deposits by the (A02-1).
