セミパラメトリックベイズ班（C01-2）

研究課題名：セミパラメトリックベイズ推論アプローチによるスパースモデリングの深化と応用

研究概要

従来のスパースモデリングでは，通常，線形モデルなど簡単なパラメトリックモデル(有限個のパラメータによる記述)によって現象が記述可能という前提をおくが，本領域が対象とする理科第2分野の実験・計測データでは，系の複雑さや計測の不確定性により簡単なモデル化が困難な場合が多い．例えば地球科学においては，対象系の物理過程はわかっているが計測過程の複雑さにより系の状態の推論が困難な場合がある．逆に脳活動計測では，計測過程は記述可能であるが対象プロセスの単純なモデル化が困難な場合が多い．

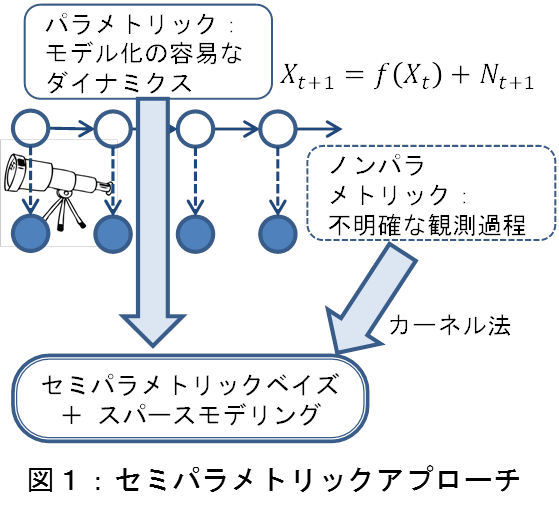
このような状況下でも対象系に関する情報を有効に抽出するためには，支配方程式や観測過程が明確な部分をパラメトリックモデルで，不明確な部分をノンパラメトリックモデル(自由度を制約しないモデル)で扱うセミパラメトリックな推論法(図1)を確立し，従来のスパースモデリングからの本質的進展をはかることが重要である．本研究では，セミパラメトリックなベイズ推論を導入することにより，新たなスパースモデリングの方法論を確立することを目的とする．

本研究に関連する国内・国外の研究動向及び位置づけ

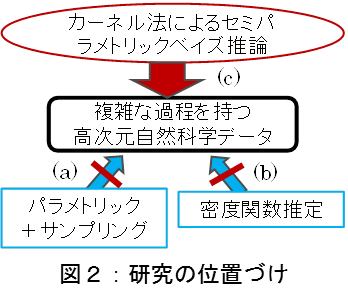自然科学データの解析では，支配方程式や観測過程に関する十分な知識を仮定してパラメトリックなアプローチを取ることが多く，その推論計算はモンテカルロ法などのサンプリング法(図2-(a))が主流である．しかしモデルの不適合や高次元データに対する計算精度・時間に大きな問題が存在する．これに対して確率密度推定などのノンパラメトリック法を組み合わせる方法(図2-(b))も研究されているが，高次元データに対する精度よい推論は困難である．本研究では，代表者が展開するカーネル法に基づいたセミパラメトリック推論(図2-(c))によって，モデルの不確実性・高次元性に頑健なスパースモデリング推論法を新たに確立する．

これまでの研究成果を踏まえ，着想に至った経緯

研究代表者の福水は，これまでにカーネル法に基づいたノンパラメトリックなベイズ推論法を開発し，部分観測マルコフ決定過程や集団遺伝学の問題などへの応用を含め，当該分野の最近の発展を牽引する研究を展開してきた．しかしながら，本領域の対象とする自然科学分野の実験・計測データに対しては，上に述べた理由により，確実性の高いパラメトリックモデルの部分と柔軟性の高いノンパラメトリック推論を効果的に融合するセミパラメトリックなベイズ推論法(図2-(c))の確立が重要であるとの着想を得た．

本計画研究の目的

自然科学分野の実験・計測データは，対象となる生体系・物理系の状態遷移を時系列的に計測する場合が多く，「状態空間モデル」として表すことができる．本研究では状態空間モデルを主要な研究対象とし，状態遷移や観測過程に不明確な部分がある場合に適用可能な，カーネル法に基づくセミパラメトリックなベイズ推論法を確立し，セミパラメトリック・スパースモデリングの方法を展開する．具体的には，今後5年間で大きな発展が望める以下の3課題に注力する．

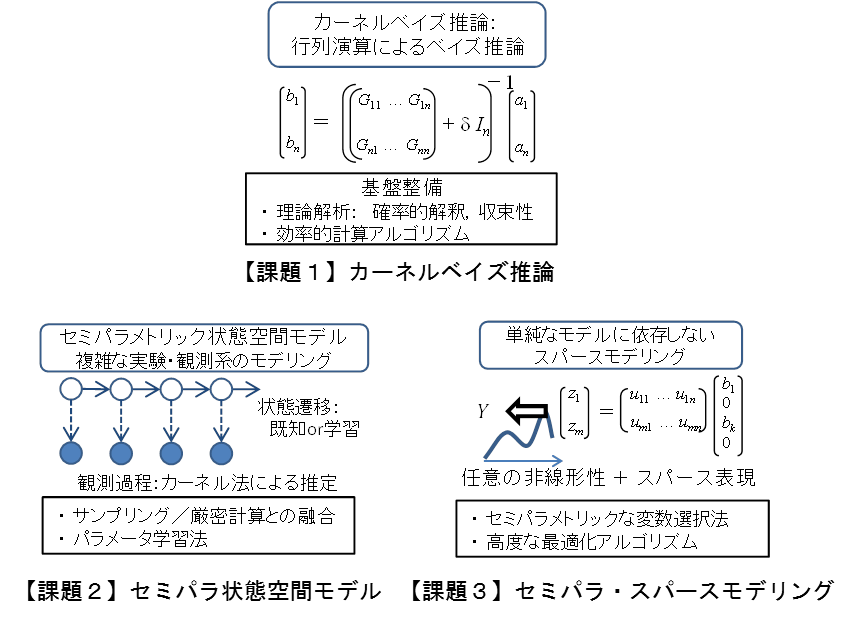
【課題1】カーネルベイズ推論の展開

本研究全体の推進に必要な理論基盤を整備するために，カーネルベイズ推論の確率論的解釈や収束性の理論解析を行う．また，大規模データへの適用を目的として，ランダム行列理論などを用いた効率的計算アルゴリズムを研究する．

【課題2】セミパラメトリック状態空間モデル

状態空間モデルにおいて，状態遷移則を既知とした場合のセミパラメトリック状態空間モデルの推論法を確立する．そのために，サンプリング法(粒子フィルタ法)との融合，厳密積分計算との融合の二つの方法を研究する．また，セミパラメトリックな設定でのパラメータ学習法を開発する．

さらに，実験G(A01, A02)で扱うさまざまな実験・計測データ，物理モデリング班(B01-3)で扱うシミュレーションデータへの応用を検討し，必要とされるアルゴリズムの改良を図るという研究ループを回し，アルゴリズムの高度化を図る．また，状態空間モデルよりも一般のモデルへセミパラメトリックベイズ推論法の拡張を検討する．

【課題3】セミパラメトリック・スパースモデリング

ベイズ的観点に基づいて，系の記述に有効な変数の選択を行うセミパラメトリック・スパース変数選択法を研究する．その際に重要となる効率的最適化アルゴリズムを，数値最適化の先端知識を駆使して研究する．

また，自然科学分野の実験・計測データはダイナミクスを対象としたものが多いため，【課題2】の状態空間モデルのようにダイナミクスを含む系に対するスパース変数選択法，および，変数間の依存関係を表すネットワークの時間的変化の推論法を研究する．さらに，これらの成果を，実験G(A01, A02)で扱うデータに応用し，必要なアルゴリズムの改良を進めるというループを回していく．