大自由度班(C01-3)

研究課題名：大規模なスパースモデリングへの統計力学的アプローチ

研究概要

情報量概念にもとづき，スパースな構造を抽出する統計モ デルによる多変量解析の方法（＝スパースモデリング）を系統的に開発／整備する．統計モデルを利用したデータからの情報抽出は尤度や相互情報量など情報量 概念に関する最適化問題として系統的に定式化することができる．しかしながら，こうした系統的定式化に沿った方法は，多くの場合，計算量的困難を伴うため 具体的に実施することが難しい．本研究では，大自由度性に起因する計算困難の問題をイジング模型など大自由度結合システムの取り扱いに長けている統計力学 の概念／技術を用いて克服することで，現状の打破を図る．具体的な事例を多数検討することを通じて，「システマティック」かつ「実践できる」スパースモデ リングの方法論を構築する．

本研究に関連する国内・国外の研究動向及び位置づけ

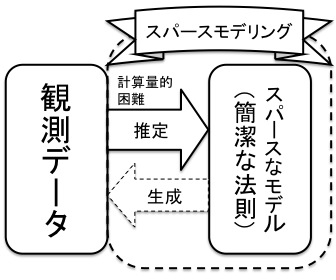
多変量解析の従来法は現実的計算量での処理の要請から，そのほとんどが“多次元正規分布”を生成モデルとして仮定している．しかしながら，現実の データは必ずしも正規性を満たさない．正規性を補完する概念として国内外の研究で近年注目されているのが「スパース性」である．ほぼすべての自然科学は，観測データ は背後にある簡潔な法則から生成されている，という考え方を共有している．スパースモデリングとは，この考え方にもとづき，データの生成モデルに簡潔性 （＝スパース性）を課すことで「観測データ→簡潔な法則」を半自動的に推定する枠組みであるが，内在する計算量的困難が情報量概念にもとづく系統的方法の 活用を阻んでいる．

これまでの研究成果を踏まえ，着想に至った経緯

我々は１９９０年代後半より一貫して，情報通信を中心とした情報科学の分野に統計力学の概念／技術を適用する研究を行なってきた． ベイズ推論の枠組みにしたがえばデータからの情報抽出も情報通信と同種の形式で定式化することができる． こうした「数理的同型性」に着眼することで， 系統的なスパースモデリングを阻む計算困難の問題も，情報通信と同様，不規則系の統計力学と構造的に類似しており，統計力学の有用性が期待できることに気づいた．

本計画研究の目的

今後５年間に大きな進展の見込まれる以下の３つの課題に取り組む．

【課題1】圧縮センシング

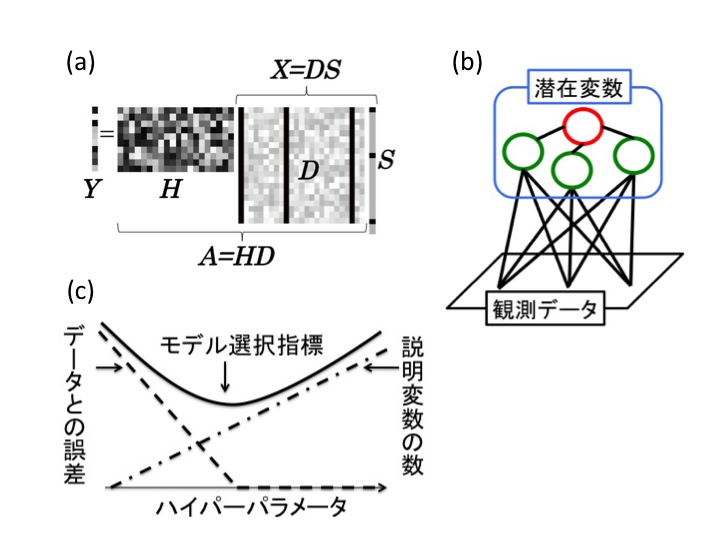
スパース性を利用して，少数の観測値からの信号復元を可能にする圧縮センシング（下図(a))はMRIやNMRなど 物理的制約から観測コストの高い問題に有用である．しかしながら， スパースな推定は一般に計算コストが高い．統計力学の平均場理論にもとづき低計算量， かつ，推定精度の高いスパース推定アルゴリズムを開発する．さらに事例研究を通じて その可能性と限界を解明する．

【課題2】潜在変数モデリング

圧縮センシングでは，スパース表現を可能にする基底が既知であることを前提としているが， より一般には観測データからこうした基底（＝簡潔な法則）を求めることが重要になる．このような課題は「潜在変数モデリング」として系統的に定式化することができる（下図(b)）． ただし，潜在変数モデリングは一般に最適化すべき目的関数が推定パラメータに複雑に依存するため実施が難しい．統計力学のレプリカ理論，平均場理論や確率推論研究の知見にもとづいてこの問題の解決をはかる．

【課題3】モデル選択

実データを解析する際には必ずデータの生成過程に関する何らかのモデル化を行わなければならないが，その結果はモデルごとに異なるため何らかの指標を用いて適切なモデルを選択することが必要になる（下図(c)）．こうした指標としては赤池情報量規準(AIC)が有名であるが，スパースモデリングではスパース性に伴う離散性，不連続性に由来して既存指標の適用がしばしば適切でない．そこで，それらに代わる指標を構成し，適切なモデル選択のための実際的アルゴリズムを開発する．