(C01-3)
The objective of this project is to develop and systemize methods of multivariate statistics that extract sparse structures lying behind observed data, utilizing the notion of information quantities. In general, one can systematically formulate the statistical-model-based information extraction as optimization problems concerning the information quantities. However, such methods are often computationally difficult to perform in practice. In this project, we intend to practically overcome this difficulty by employing methods and notions of statistical mechanics, which has been constantly growing to encompass the many new skills needed to handle massive statistical models through tackling the many-body problems in physics. By analyzing various concrete models, we aim to construct a methodology for "systematic" and "practically performable" sparse modeling.
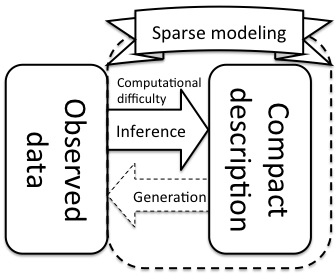
In the current theory of multivariate statistics, most methods assume their generative models as multivariate Gaussian distributions due to the unavoidable constraint of practical feasibility. However, realistic data do not necessarily have "Gaussianity". In recent years, "sparsity" has drawn attention as a concept that complements Gaussianity. Most of the natural sciences share the idea that observed data is generated from a certain simple law. Sparse modeling is a formalism to semi-automatically infer the simple laws from the observed data by imposing the sparseness to assumed generative models. However, computational difficulty underlying high-dimensional statistical models has prevented us from utilizing the systematic methodologies based on the notion of information quantities.
Since the late 1990s, we have continuously applied statistical mechanics to resolve computational difficulties arising in various problems related to information science, such as error correcting codes, data compression, wireless communication, etc. Following the framework of Bayesian statistics, one can systematically formulate information extraction from data as well as problems of communication. By focusing on such structural similarity in the mathematical formulations, we realized that one could also use statistical mechanics to systematically overcome the computational difficulty in performing massive sparse modeling.
We will work through the following three subjects, which are expected to significantly develop in the coming five years.
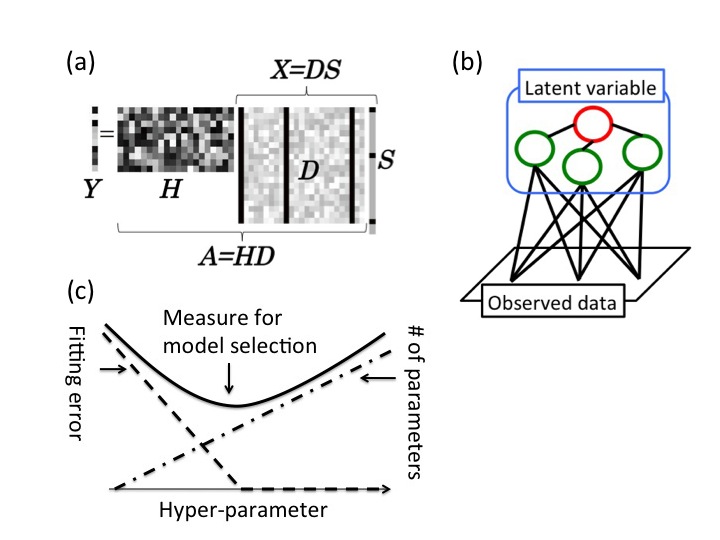
- [Subject 1] Compressed sensing
Compressed sensing (CS) is a scheme of signal processing that enables an accurate signal recovery from much fewer measurements than before by using the prior information of "sparseness" of the objective signals. Although it is expected to be considerably useful for various problems in which physical measurements are costly, such as NMR and MRI, the inference of the sparse signals generally requires large computational costs. For practically resolving this difficulty, we are developing computationally feasible and accurate approximation algorithms for the signal recovery on the basis of the mean field theory of statistical mechanics. We also examine the possibilities and limitations of such algorithms through the investigation of various model systems. - [Subject 2] Latent variable modeling
The basic setup of CS assumes that a basis representing the sparseness of the objective signals is known. However, in various situations, it is important to find such a basis from a given set of data. Problems of this kind can be formulated systematically as "latent variable models". Unfortunately, the execution of latent variable modeling is non-trivial because the objective function to be optimized in the modeling generally depends upon the latent variables in a complicated manner. We tackle this problem using methods and notions from statistical mechanics. - [Subject 3] Model selection
Whenever we analyze real data, we need to assume a certain model concerning how the data generation is processed. When multiple models are tested, it is necessary to select the most reliable candidate from among them. The Akaike information criterion (AIC) is one of the most famous measures for such model comparison. However, using AIC is not necessarily justified theoretically for sparse modeling, for which the statistical regularity assumed in the derivation of AIC is not guaranteed. To resolve this problem, we propose alternative measures based on the knowledge of singular statistical models and develop practically feasible algorithms for the model selection.